Optimizing Bloom Filter: Challenges, Solutions, and Comparisons

2018 综述类文章 IEEE Communications Surveys and Tutorials

对该文章的阅读是出于实现需求的，因此进行了大量的节选并加入了个人主观判断。主要记录的内容为各种不同过滤器的原理与实现，以及特点。如有其他需求还是阅读原文为好。

其他论文：Cache-, hash- and space- efficient bloom filter

摘要

对该问题给出了比较精确的定义：membership query，判断给定元素x是否为给定集合S的一员。

BF的特性：空间利用高效+常数时间查找

从两个方面对BF(bloom filter)的变体进行总结：performance和generalization

• Performance：降低false positive和实现代价
• Generalization：使其更加泛用（diversifying the input sets and enriching the output functionalities）

Intro

BF的challenge: false positive, implementation, elasticity, functionality to some content

会从下面四个角度：

• techniques to reduce the false positive
• optimizations in a real implementation
• dedicated desings for diverse dataset
• proposal to enable more functionalities

文章有以下内容：

• Section2，analyze challenge issue
• Section3，application of BF
• Section4，variants designed for reducing false positive
• Section5，implementation optimization
• Section6，generalizing the set diversity
• Section7，functionality enrichment
• Section8，analyze and compare
• Section9，Summary+open issue
• Section10，Conclude

Section2 Bloom Filters

特性：

• space-efficient：BF的主要功能由m-bit的向量提供，其中m与元素数量n成正比且与元素的大小无关。（Equation2计算）
• Constant time query：O(k)级别，比数或者列表还要快。
• one-side error：只有false positive的可能，而没有false negative的可能

Challenge:

• false positive：即BF认为可能在集合中的元素有可能并不存在于集合之中。解决方案是使用更多的内存和复杂的操作，或者对误报的元素进行拯救(remedy)
• Implementation：在实际实现中部分实现会成为瓶颈；一般来说只有一半的bit会被置为1（即占用率不会超过一半）；高性能的哈希函数需要较大的时间复杂度，对轻量应用不友好
• Elasticity：参数m,n,k和所选择的哈希函数都是预定义的，bit设置之后也不能修改（经典结构）
• functinoality：经典BF只支持插入和查询

Section3 Application of BF

跳过，没什么意思。

Section4 Reduce of False Positive

因为false positive这一部分实在是比较重要，所以优先看了一下。

定义：false positive proportion(FPP)与false positive rate(FPR)

• FPP是经验概念，是false positive error与总query数之间的比例
• FPR是理论概念，即任意query可能出现false positive error的概率。

一般来说FPP基于对FPR的估计得到，FPR是一个常数，由BF架构自身决定（m、n与k）

4.1 Reducing FP with prior knowledge

引入先验知识。对于query的元素集合Q，一个经典的场景是multicast routing（路由问题）

根据先验知识选择哈希函数，来达到最少的FPP。

• multi-class BF：作者观察到对于不同的元素来说false positive的代价不同。具体来说更高出现概率的元素其false positive的代价会更小。对于每个元素采用不同数量的哈希函数来最小化falsely matched elements的期望数量。（场景应该是in-switch routing problem）
• Bloom paradox：一种现象。设M，C和T分别为在主存，缓存和在主存但在访问BF时结果是正确的。所以​，其中​是false positive proportion。而在M的大小为十的十次方，C的大小为十的四次方且FPP为千分之一的时候，FPR会接近于1-10^-3，即基本全都是false positive
• Optihash：在Publish/Subscribe Internet Routing Parading问题中新设计，用于扩展原有的BF。
  • 介绍，由三个部分组成，一个bit array w，两个整数alpha和beta。
  • 要求已经知道元素集合Q，可以求得一个最小的false positive集合F。
  • 原理没看明白

4.2 Reducing FP With the One-sided Error

利用BF没有false negative error的特性，即判定x不在集合S中的准确率为100%。

下列方法对于动态增加与删除的支持可能都存在问题，因此需要再做扩展。

• 更多的检索来降低false positive。一个例子：在字典树Trie中，如果能够提前检查出某个节点是否在树中，能减少访问Trie的次数（即只在节点存在于Trie时进行访问）。但是false positive的存在使得额外访问的情况不能断绝。一个想法是，一个节点的存在必然包含着一个前置节点，因此请求节点的同时也请求前置节点（Trie的性质，比如"bitcoin"存在，则"bitcoi"也肯定存在）就可以极大降低false positive的情况。
• Cross-chekcing BF：
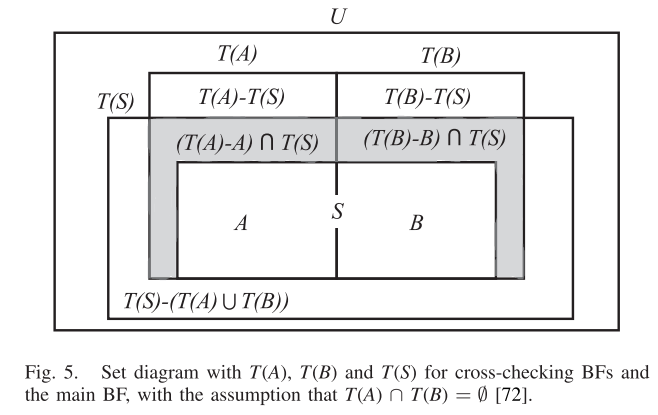
  • 由一个主要的BF和多个cross-checking BF构成。主要的BF中包含了所有元素，设为集合S。不同的cross-checking BF之间没有交集，比如Fig5的A和B，相交为空集，并为S。
  • 判断x不在集合S中，需要集合A和集合B判断x不在它们之中，准确率为100%（当然，直接用S判断也可以，但是S这个主结构应该不用实现出来）
  • 判断x在集合S中比较复杂。设T(S)等表示一个能够返回Positive的元素集合。通过访问A和B，false positive可以变成​ 。即要求对于任意元素x，判断其存在的标准为其在集合A或者集合B中。
  • 这个操作能够降低理论上的false positive rate，详见论文。该操作最重要的一点是它可扩展性很强，几乎所有方法都能够尝试这种改进。虽然看上去需要知晓所有元素才能完成切分，但是可以考虑使用分桶或者哈希的方式来保证不同元素绝对只会进入对应的BF中，因此是具备泛用性的。

• Complement BF：该方法提出是为了减少哈希表的访问频率（存在一个大的哈希表）。与Cross-checking BF不同，该方法只有两个互不相交的集合S和S^C（需要知晓全部元素）。如果一个元素不在S中，它一定在S^C中。有四种情况。 1. main BF为真且Complement BF为假，则x在S中 2. main BF为假且Complement BF为真，则x不在S中 3. 如果都为真，则访问哈希表，付出代价 4. 都为假的情况是不存在的，因为是one-side error。 5. 总结：这个方法的假设是比较强的，只有在知晓所有元素的情况下才能够使用。
• Yes-no BF：BF不只是保留需要的元素S，还保留那些会导致false positive的元素。
  • 由两个部分组成：
  • yes-filter存储集合S的元素
  • no-filter存储false-positive的元素
  • 总体有m bits，分为两个部分：p bits为yes filter，r*q bits分给r个no-filter，每个filter有q bits
  • yes filter如正常的BF。
  • no filter捕捉造成false-positive的元素，存储在其中一个no-filters中
  • 此处，如果x在集合S中，当且仅当yes filter中全为1（正常BF的判断）且no filter中全为0
• 优点：
  • 反向利用了false positive单边错误的性质，只要false positive的情况出现过就不会出现false positive
  • 即对每个元素而言，false positive的情况只会出现一遍。
• 缺点：
  • no filter可能会很大，这个视情况而定。
  • 可能会有非常频繁的读写
  • 这个假设其实有点类似于之前Complement BF的假设，只是它可以允许其动态成立。对于全集变动不大的情况是比较好的。

4.3 Reducing FP via Bit Resetting

从根本上来说，false positive出现的原因在于BF检查每个1的时候是没有去区分被放入到不同位置的元素，因此当一个元素所需要的位置全部被置为1时其可能被视为false positive

引入false negative？

• Retouched BF：通过将1置0的方式来降低false positive，数量和位置均为随机。
• Generalized BF：设置两类hash函数：g和h。g会将所映射到的位置的bits置为0，h会将所映射到的bits置1。对于一个结果，如果所有的g都是0且h都是1，则返回positive，如果有一个不符合，则为negative
• Multi-partitioned Counting BF：对CBF的改进。CBF引入了插入和删除操作来支持动态的数据集。为了降低内存访问的次数，将m个cell分为l个word，每个wrod可以由一次内存访问得到。这样只需要再加一个哈希函数来做映射，将每个元素x固定分派到其中一个word中。
  • 作者称该方法会导致更多的false positive错误，对此需要在每个word中采用层级结构。第一层用作member ship query，后续层用于维护层级的性质。

4.4 Reducing FP with selected hash functions

False positive的不可避免性是源于潜在的哈希碰撞。一般来说，false positive rate与bit vector中被设置为1的bit数量是成正比的。

不太看好这个方向。

• 引入 the power of two choices，即直接引入两组或更多的哈希函数，插入时会选择增加最少1的那组。在membership query中只要通过任意一组即成功。
  • 但是这样false positive肯定是会上升的。我觉得与BF一般的false positive原因相比，哈希碰撞所造成的原因是不足道的。
• partitioned hash scheme，基于balls and bins theory。即在插入之前对集合S应用哈希函数，将其分为g个独立的group……
• EGH filter：将k个哈希函数替换成k个更简单的函数，基于k个素数。这种方法对于一个严格限定的元素数量集合可以达到false positive free，详见Bloom Filter with a False Positive Free Zone
  • EGH相比于BF而言是决定性的，速度更快。但是确定的false positive free zone是相对比较小的，m=2127 bit和k=34个hash function只能够确认一个free zone，包含20个不同的元素，集合中最多有562个元素。且数量超过上限是仍然会出现false positive。
  • 因此，只在强烈需要避免false positive的时候才推荐使用。

4.5 Reducing FP by Differentiated Representation

CBF也会有false positive，因为它无法区分每个coutner的记录是来源于哪些元素的。

通过添加额外的空间与结构，以期望对不同key所产生的结果进行区分。

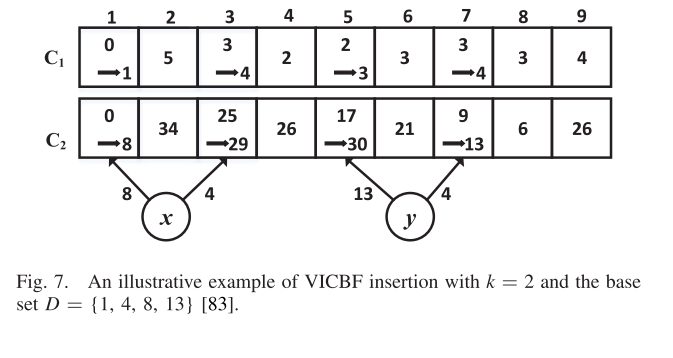
• Variable-increment counting BF(VI-CBF)：每个counter的增加使用一个hash variable increment，而不是原有的unit increment（即原有的对应counter加1）
  • 整体结构由两个Counter vector组成
    • 第一个counter vector：C1，记录每个位置的元素数量
    • 第二个counter vector：C2，记录该位置元素的加权和
    • 加权和权重的选择部分没太看明白，大意上是对元素进行分桶，选出k个不同的increment（g）；位置选择采用哈希函数h系列。
      • C1部分中哈希函数h对应的位置全部加1.
      • C2部分中哈希函数h对应的位置加k个g系列哈希函数的和。
    • 检查元素是否存在：
      • 若C1中有对应counter为0，肯定不在
      • 若C2中对应位置的元素数量很小，则可以进行推断（比如只有1）。如果C2中对应位置的值与query key哈希的结果一致（只有一个）或者可能得到(>1)，则有高概率认为元素存在；如果存在很多值则认为这个counter没有价值。
    • 优点：支持动态插入删除（应该），false positive rate应该会有效降低
    • 缺点：对于大规模数据不友好（C2数组可能会溢出，需要严谨的计算和限制）

• Fingerprint counter BF(FP-CBF)：使用唯一的Fingerprint对元素进行标记。每一个cell包含两个Field：fingerprint field和counter field。
  • fingerprint有a bits，存储映射到该cell的fingerprint。由一个哈希函数组成，将元素x映射到0~2^a空间中。
    • 更新时，通过XOR操作新加入的与已知的数据
  • counter field有c bits，记录存储的数量
    • 更新时加1
  • 在查询的时候：
    • 如果counter field的对应元素没有全大于等于1，则返回false
    • 如果counter filed的对应元素全部大于1，则检查fingerprint field
      • 如果对应元素中数量为1，则检查fingerprint是否相同
      • 不然转为一般情况，不可识别
    • 优点：支持删除操作，异或操作是可逆的。（两次异或操作即可以得到原来的值）
    • 缺点：其性能对超参数（元素数量n，counter个数m，哈希函数个数k）特别敏感，如果有大量元素其全部Counter数量都大于1，则fingerprint几乎无法发挥所用。

Section 5 Optimization of implementation measurements

提升BF的性能：计算复杂度、访存次数、空间占用（或者有效占比）、能量消耗（平均代价？）

5.1 Computation optimization

BF的计算代价主要来源于两个方面：哈希函数的计算代价与处理请求的判断过程。哈希函数（MD5、SHA-1）的计算代价是较大的，具有特殊性质的哈希函数计算代价尤其大。现有的最新方法希望通过一个或两个哈希函数来产生多个独立的哈希值。

• Less hash, same performance：使用两个伪随机的哈希函数来产生额外的哈希函数。
• One Hash BF（OHBF）：可以使用一个哈希函数产生k个哈希值。将哈希过程看作是两个步骤，第一步将输入元素映射到机械码（32bits, 64bits…），第二步使用求模的方式将机械码映射到指定空间。
  • OHBF将产生的m-bit vector切分成k个不同 的模块，比如$m = m_1+m_2+…+m_k$，其中$m_i$即为第i部分的长度。每次对指定部分进行求模即可。
  • 缺点：会破坏哈希的随机性，因为哈希函数的变化可能只是局限于某个范围而不是整个bit vector，因此可能导致更多的哈希碰撞或者更高的false positive rate。
  • 作者也提到了，当m提高的时候，各项指标与标准BF会逐渐接近

另一种想法是加速哈希或者检验的计算，一般的想法是并行化处理，比如将bit vector切分成多个段后对每一段进行同步处理。

• DLB-BF：用于IP最长前缀查找，策略是采用多个等长度的BF进行分组等。因为与需求偏差较大，暂时略过。
• Combinatorial BF：假设S中存在多个group,并且需要指出元素不仅属于其中的哪一个group。偏差较大，暂时略过
• Ultra-Fast BF：尝试对哈希函数和检验过程进行直接加速。其向量由r个块组成，每个块有b个bit，k个连续的word，因此b = k * w，其中w是word的长度。总bits数量m=rkw。
  • 为了插入元素x，哈希函数h_0会随机选择r个block中的一个。接下来，元素x就会被k个哈希函数分别映射到k个word中，查询时同理。
  • 如此，算法使用了SIMD(Single Instruction Multiple Data)的模式来在k个哈希函数的计算中引入并行化，基本想法是使用一个哈希函数来产生多个哈希函数值；而在查询的时候天然具有并行性，因为数据必然存储在同一个block的k个不同的word中。
  • 问题：哈希函数的数量与word的数量似乎是等同的，不确定是否是笔误。

5.2 Memory access

为了完成membership query，每次查询的时候都需要读k个bits。在一些特殊的结构下还需要反复访存（比如索引结构）。因此一些方法被用来减少访存的次数。

• Bloom-l：方法由l个word组成，每个可以通过一次memory access拉到处理器中（应该是小于CPU缓存大小）。在插入元素x前，可以通过hash函数产生一系列的哈希值，其中log_2(l)个hash bits用来选择x所需要的word，k*log_2(w)个hash bits将x映射到指定word的k个位置中，并将这k个位置的0置1。
  • 这样，进行查询的时候每次也只需要CPU从内存中进行一次访存。
• OMASS：OMASS关注set sepration问题，即确定元素x属于那个集合。现有的方法采用的是并行的BF，但这样会导致过多的访存。
  • 一个想法是使用全局哈希函数将其映射到block，每个block只有32bits或者64bits ，并同时访问s个query sets来加速。
  • 更进一步的改进，OMASS将每个block切分成k个sub-block，每个sub-block与哈希函数对应（第j个哈希函数的结果一定在第j个block上）。同时为了防止内存共享带来的干扰，对同一哈希函数的值进行打乱：​，其中i是不超过s的整数，b是sub-block的大小
  • 此时，对于单个元素x的插入和检验不会影响到其他s-1个集合，因此一次内存访问可以同时解决多个query set。

5.3 Space Efficiency

空间有效性问题，因为可能需要在本地存放BF或者需要在分布式系统中散步BF，因此需要尽量降低BF的内存占用。

PS：为了达到最小的false positive rate，标准BF的bit utilization只有50%。

这个问题比较关键

• compressed BF：没看明白。原文说Compressed BF optimize transmission overhead，当filter需要在网络中进行交换。可filter为什么需要在网络中交换我有点没搞明白，压缩的话直接用文件压缩方法为什么不行呢？
• Compacted BF：同上。
• d-left counting BF：为了解决CBF高false positive rate和space overhead的问题，而dlCBF采用了d-left hash function，号称是”几乎最完美的哈希函数(almost perfect hash function)“。
  • 对于静态的集合S，可以由一种方式来计算出一个完美的哈希函数使得其绝对不会发生碰撞（结果比较复杂，略过，这个内存占用比bloom filter还少）。但是对于动态集合来说是不可行的，因为每一次插入或删除都会导致整个哈希表的重构。
  • d-left hash table，与其说是变体不如说更像是trick。以2-left hash tables为例，它同时有两个哈希表，每次插入的时候选择更少的那边进行存储（相同则选择最左边），查找的时候两边一起查找。（注意：考虑的时候只考虑对应位置上的哈希个数，而不考虑子表中已有的哈希个数。即仅考虑哈希的碰撞次数）
  • dlCBF将cell vector切分d个子表，每个子表含有n/d个buckets，其中n是buckets的总数。每个bucket有c个cell，每个cell有一个fingerprint域和一个counter域。
    • 元素x的fingerprint由两个部分组成，第一部分由bucket的index构成（即x的位置）；第二部分是x的一部分remainder
    • 具体来说，插入元素x的时候会使用哈希函数生成一个字符串，并将这个字符串分为d+1段。其中的d段用作选择d个哈希表的候选位置，最后一段作为remainder构建Fingerprint。
    • 如此，x的remainder会被插入到所有位置中负载最小的区域（即counter域最小的区域）
    • 检索x的时候，所有的d个cell都会被检查。如果发现了x的remainder，则找到；不然就是没有找到。
  • 网上的数据显示，CBF可以达到标准BF的四倍，而d-left BF的内存占用只有CBF的一半甚至更少。
  • 实现难度：10%，因为找到了一份go的github代码，而且基础思想确实是相当的简单。
  • L-CBF: A low-power, fast counting Bloom filter architecture，复杂度和实现都比较接近，可以参考一下。
• Memory-optimized BF：考虑到标准BF采用k个哈希函数在k个内存位置上放置自己的数据，该方法使用了一个额外的哈希函数，在这k个哈希函数中选择一个新的值。（大致的思想真的是这样，不如说为什么原本需要k个哈希函数？我个人觉得是出于哈希碰撞层面的考虑，但一个哈希函数与该方法又有什么样的不同呢？）
• Matrix BF：用于检测文档中的复制粘贴内容，比较复杂，没看明白。
• Forest-structed BF：可以存放在SSD中的BF。更加复杂。

5.4 Energy Saving

略过，这方面应该与需求非常不符合。

Section 6 Representation of diverse sets

输入的特征可能具有特殊的性质，因此在不同的场景中，会有不同的特殊处理方式。

例如：

• 如果数据集是一个multiset（允许重复元素），则需要记录元素重复的次数
• 如果输入数据集是动态的，则BF capacity需要根据需求伸缩
• 如果输入数据集的元素具有不同的权重，则需要确保高权重的元素具有更低的FPR。
• 如果输入数据集的元素并不是完全独立，而是具有某种逻辑、时序或空间结构，则应该将其利用起来。（比如已知元素都在一个Trie中，即一个元素的前缀也必定在集合之中）

这一章可能需要对需求进行进一步解析才能有进一步阅读的机会，至少现在我觉得没什么必要。

除了第二部分

6.1 Multisets

6.2 Dynamic Sets

BF是为静态数据集设计的，但是动态数据集

• Variable length signatures
• Dynamic BF：由多个同构的BF组成
  • 一大问题是false positive rate很高
• Scalable BF：由多个异构的BF组成
  • 一大问题是内存消耗大，哈希计算代价高
• Dynamic BF Array：DBA
  • 2011
  • 由多组BF组成，每组BF中有g个同构的BF，因此DBA天然支持并行化，因为不同组的BF之间不会相互影响。
  • 删除的时候，因为大规模存储系统一般在off-peak的时候才会去删除过时的数据，因此DBA可以给每个BF设置一个预定义的阈值来批量完成删除操作。
  • false positive是可控得到，但是需要增加每个BF的长度或者减少BF的数量。而且不支持在线删除。
  • 会引入false negative
• Par-BF
  • 2016
  • Par-BF也是由sub-BF的列表组成，每个sub-BF由多个同构的BF组成。
  • 插入元素的时候，Par-BF会定位到活跃的sub-BF并设置对应的比特位为1
  • 删除则在指定的sub-BF将这些位置为0。但该操作不会引入false negative，理论上操作复杂度与DBA类似。

6.3 Weighted Sets

6.4 Key-value

6.5 Sequence Sets and Spatial Sets

Section 7 Functionality Enrichment

标准的BF只支持membership query，因为bit vector只能够保存每个元素的所属信息。与输入集合相同，输出集合也可以在不同的场景下得到强化。

7.1 Element Deletion

顾名思义，需要允许系统从BF中删除元素，并允许添加其他新的元素。

如果我对需求没有理解错的话，其实是可以不用删除操作的。

7.2 Element Decay

对于在线的系统来说，新的数据应该具有更高的权值，为此需要逐渐将旧有的数据退化。（当然，这方面可能微信文章阅读数统计方案中采用的方法会更合适，即每隔指定时间采用一个新的BF，过期淘汰或者过时降权）

没有需求，但是后续可能有

7.3 Approximate membership query

与准确的所属查询不同，近似所属查询需要回答x是否足够接近S中的元素(Is x close to an element in S)

没有需求

7.4 Enrichment of BF Semantics

BF的一个天生缺陷在于，其只存储了所属信息，而无法包含元素的其他信息。

应该没有这方面需求

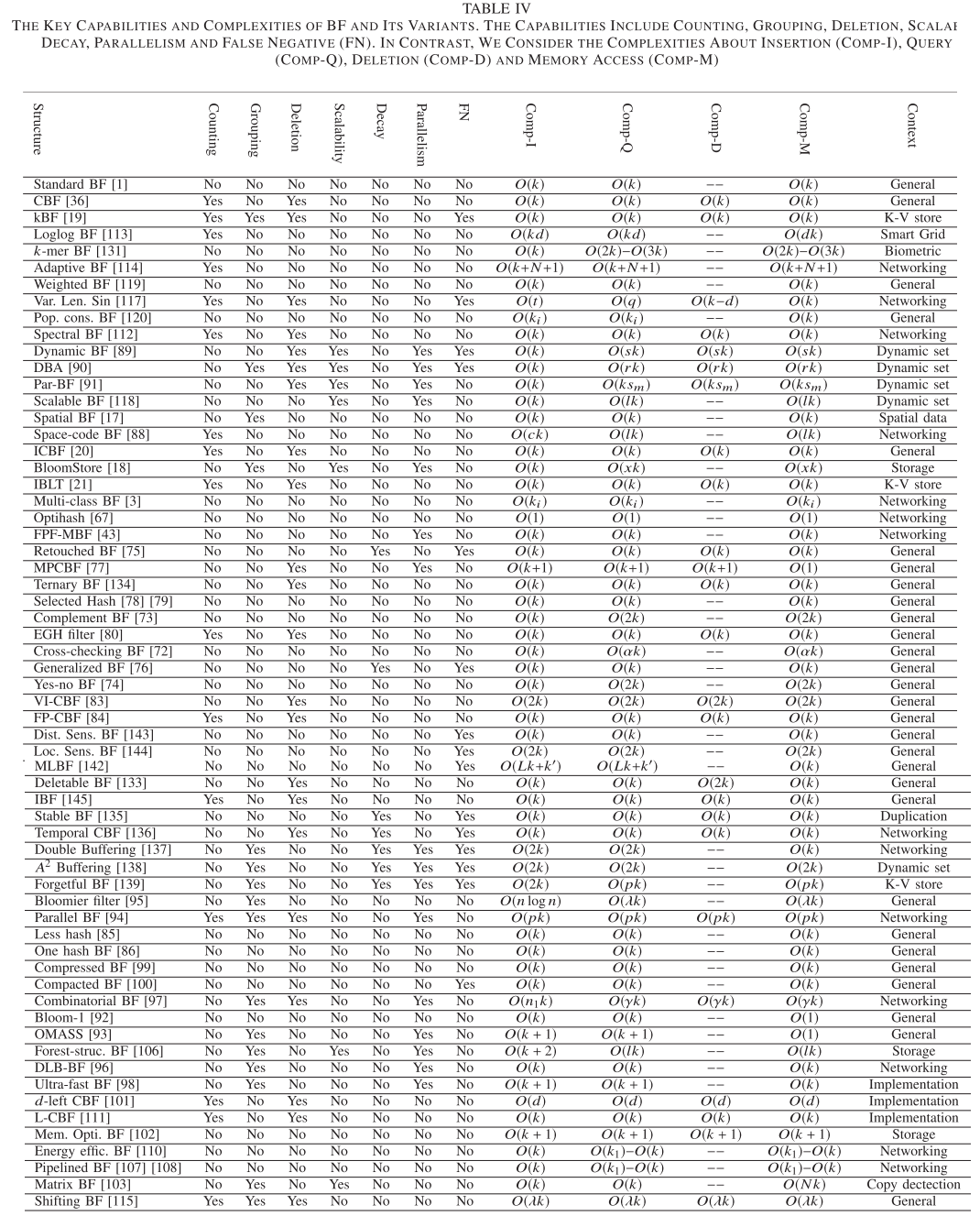
Section 8 Classification and comparison

（一般对于综述文章而言这一部分是最重要的，除非主做该领域的，基本没有人能够读完所有论文，所以只能指望综述作者有一套成熟的评价方案了）

Section 9 Summary and open issues

open issue

• Extension or downsizing at arbitrary scale：对于现有的支持扩展或缩小的结构（DBF、DBA、Matrix BF、Scalable BF）都是对整个结构进行的，即只能对sub-BF结构进行增加或者删除。那如果只是一个元素增加就要对整个结构进行修改， 肯定是不经济的。
• Representation of inter-element relationship：现有的BF结构对于元素的存储表示都是独立的，这方面的例外是一些使用locality sensitive hash function的例子。因此现在需要有BF的变体，不只是能够记录元素的membership，也能够表示内部联系。这样的话就能彻底解决false positive的问题。
• Alternates of BFs：除了从BF本身的结构出发，也可以直接修改底层结构。比如Cuckoo filter（布谷鸟过滤器）、Quotient filter和其变体
  • 与BF结构不同，这些结构直接存储了元素的fingerprint（即存储信息与元素值相关，而不是仅与元素出现频率相关）
• Extensive applications of BFs: 更多领域的应用。